Identifying special situations in factoring

• Difference of two squares
• a²- b² = (a + b)(a - b)
• (x + 9)(x − 9)
• (6x − 1)(6x + 1)
• (x³ − 8)(x³ + 8)
• Trinomial perfect squares
  • a² + 2ab + b²= (a + b)(a + b) or (a + b)²
    • x²-4x+4
    • 16x² - 8xy + y² = (4x - y)²
    • x²+6x+9
  • ^{a2 - 2ab + b2 = (a - b)(a - b) or (a - b)2}
• Difference of two cubes
  • a³ - b³
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • 
        
        
        
        
        Sum of two cubes
• • a³ + b³ 
  • • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • 
• Binomial expansion
•  

End Behaviors/Naming Polynomials

Linear Equations: 

y= mx+b 

1 degree

0 turns 

Domain - x values
Range - y values referred to as f(x)

When m is Positive: 

domain → +∞, range → +∞ (rises on the right)

domain → -∞, range → -∞ (falls on the left)

When m is Negative 

domain → -∞, range → +∞ (rises on the left)

domain → +∞, range → -∞ (falls on the right)

Quadratic Equations (parabolic equation)

y=ax² 

2 degree 

1 turn

(a+b)(c+d)

            

When a is Positive 

When a is Negative 

Naming Polynomials: 

--Number of turns is always 1 less than the degree. 

Degree:

0- Constant 

1- Linear

2- Quadratic 

3- Cubic

4- Quartic

5- Quintic 

6 to ∞- nth Degree 

Terms:

Monomial 

Binomial 

Trinomial 

Quadrinomial 

Polynomial 

domain → +∞, range → -∞ (falls on the right)

domain → -∞, range → -∞ (falls on the left)

domain → +∞, range → +∞ (rises on the right)

domain → -∞, range → -∞ (falls on the left)

Quadtratic Equations:

How to identify quadratic equations:
ax² + bx + cy² + dy + e= 0

If there is an equation like 4x² + 4y² = 36 then it is a circle  because a=c. The a is 4 and the c is 4

If there is an equation like 2x² + 4y = 3 then it is a parabola because a or c equals 0

If there is an equation like 4x² - 4y² = 12 then it is a hyperbola  because a and c have different signs.

If there is an equation like 4x² + 3y² = 25 then it is an ellipse because a is not equal to c, and the signs are the same.






this is an ellipse. 

Multplying Matrices.

There are 3 steps to multplying matrices.

1) Write a dimension Statement

2) Row x column and Sum x products

3) Repeat until complete

For this picture, you would have to repeat this process for the 2nd row x 4th column 

Dimensions of Matrices

 

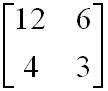
This is a 2x2 matrix. It has 2 rows that go side to side. 2 columns that go side to side.

 

This is a 3x2 Matrix. It has 3 rows and 2 columns

 

  

This is a 3x3 matrix. 3 rows by 2 columns 

This is a special kind of matrix. It is called an Identity Matrix.   It serves as the multiplicative identity. 

Error Analysis

 In this picture, the error is in the equation. First off, it is not in slope intercept form which is y=mx+b and the points wouldn't match when you plug them into the equation. The correct answer should be y=2x+9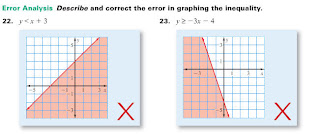 

The problem in number 22 is that the line should be a dashed line and not a solid line, and in 23 the other side of the boundary line should be shaded. 

You have to plug the solution of equation into both equations. So if you plug (1,-2) into x+4y=-5  it does not work. 

In problem 20, the boundary line should be a dashed line and not solid, and in 21 the bottom half of the boundary line should be shaded.

Graphing y=a|x-h|+k

For this equation the Vertex would be: (h,k)
The variable a represents whether the graph opens up or down. 
The h moves the graph to the left or right.
The k moves the graph up or down. 

Examples: 


When you have the equations:

•  y = |x + h| the graph will move h units to the left.

• y = |x - h| the graph will move h units to the right.
    
•  y = |x| + k the graph will move up k units.
• 
  
•  y = |x| - k the graph will move down k units. 

If your equation happens to have a negative sign in front of the absolute value, the graph will be flipped or reflected over the x-axis